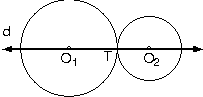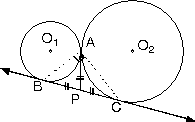- TEĞET - KİRİŞ ÖZELLİKLERİ
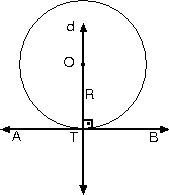
1. Teğet noktasından
ve çemberin merkezinden geçen doğru, teğet olan doğruya
diktir.AB doğrusu T noktasında çembere teğet
Teğet doğrusuna, teğet
noktasından çizilen dik doğru çemberin merkezinden
geçer.
|
 |
2. Çemberin dışındaki bir
noktadan çembere çizilen teğetlerin uzulukları birbirine
eşittir.
|
[PA ve [PT
çembere teğet
|
 |
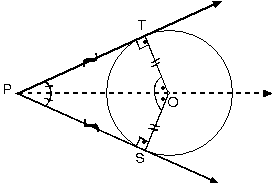
[PT ve [PS çembere teğet ve O çemberin
merkezi ise [PO, TPS açısının açıortayıdır.
|OT| = |OS| ve [PT] ^
[TO], [PS] ^ [SO]
olduğundan PTOS dörtgeni bir deltoid tir.
- İçten ve dıştan teğet çemberlerde
merkezleri birleştiren doğru teğet noktasından
geçer.
| O1
ve O2
merkezli çemberler T noktasında dıştan teğet
ise, merkezleri birleştiren doğru T noktasından
geçer. |
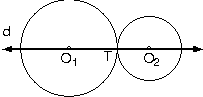 |
| Aynı özellik içten teğet
çemberler için de geçerlidir.O1
, O2
ve T noktaları aynı doğru üzerindedir. |
 |
| 3. Bir çemberin
merkezinden kirişe indirilen dikme, kirişi ortalar. |
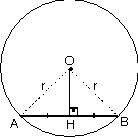 |
Bir çemberde, merkeze uzaklıkları
eşit olan kirişlerin uzunlukları da eşittir.
|
 |
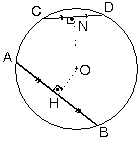
Bir çemberde herhangi iki
kirişten merkeze yakın olanı daha büyüktür.
|
 |
4. Bir çemberde eşit
uzunluktaki kirişlerin gördüğü yaylarda eşittir.
|
 |
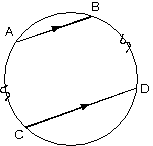
| 5. Bir çemberde
paralel iki kiriş arasında kalan yaylar
eşittir.
|
 |
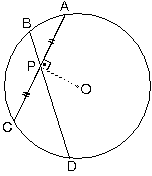
Bir çember içinde alınan
herhangi bir P noktasından geçen en kısa kiriş,
orta noktası P olan kiriştir.
|
 |
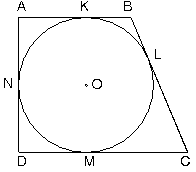
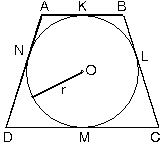
| 1. Bir çembere teğet
dört doğru parçasının oluşturduğu
dörtgene teğetler dörtgeni denir.
ABCD dörtgeninde K, L, M, N teğetlerin
değme noktasıdır.
|
 |
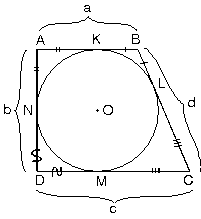
| 2. Teğetler dörtgeninde
karşılıklı kenarların uzunlukları
toplamı eşittir.
|
 |
| 3. Teğetler dörtgeninin
alanı; içteğet çemberin yarıçapı ile çevresinin
çarpımının yarısıdır.
|
 |
|
Kirişler dörtgeninde karşılıklı
açıların toplamının 180° dir.
Dörtgeninin alanı;
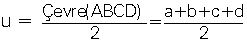
| A(ABCD)=Ö(u
- a)(u - b)(u - c)(u - d) |
|
 |
KUVVET
1. Çemberin Dışındaki Bir
Noktanın Çembere Göre Kuvveti
|
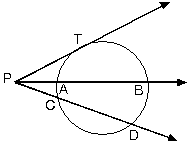
[PT, T noktasında çembere teğet,
[PB ve [PD çemberi
kesen ışınlar
| Kuvvet = |PT|2
= |PA| . |PB| = |PC| .
|PD| |
|
 |
2. Çemberin İçindeki Bir Noktanın
Çembere Göre Kuvveti
| Bir çemberin içindeki bir
noktada kesişen iki kiriş üzerinde,
kesim noktasının ayırdığı
parçaların uzunlukları çarpımı
sabittir.
| Kuvvet = |PA| . |PB|
= |PC| . |PD| |
|
 |
- Çemberin üzerindeki bir noktanın
çembere göre kuvveti sıfırdır
3. İki Çemberin Kuvvet Ekseni
Kuvvet ekseni üzerindeki noktaların her
iki çembere göre kuvvetleri eşittir.
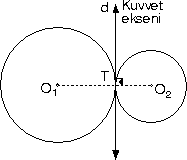
| a. Dıştan teğet
iki çemberin kuvvet ekseni teğet noktasından geçer.
Kuvvet ekseni çemberin merkezlerini birleştiren doğruya
teğet noktasında diktir.
|O1O2|
= r1
+ r2
|
 |
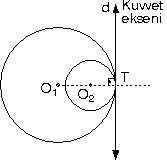
| b. İçten teğet
çemberlerin kuvvet ekseni teğet noktasından geçer.
Kuvvet ekseni merkezlerden geçen doğruya teğet noktasında
diktir.
|O1O2|
= r1
– r2
|
 |
| c. Kesişen çemberlerde
kuvvet ekseni çemberlerin kesişim noktalarından geçer
ve merkezleri birleştiren doğruya diktir.
|O1O2|
< r1
+ r2
|
 |
şekildeki P noktasının
A noktasında birbirine dıştan teğet olan O1
ve O2
merkezli çemberlere uygulamış olduğu kuvvetler eşittir.
| |PB|=|PA|=|PC| Û
|BA]^[AC] |
|
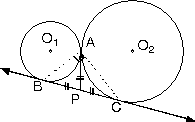 |
- Yarıçapları kesişim
noktalarında dik olan çemberlere dik kesişen çemberler
denir.
| d. Kesişmeyen çemberlerin
ortak noktası yoktur. Kuvvet ekseni iki çemberin arasında
ve çemberlerin merkezlerini birleştiren doğruya
diktir.
|O1O2|
> r1
+ r2
|
 |
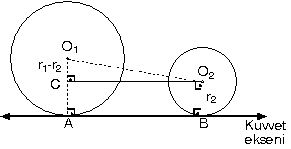
4. Ortak Teğet Parçasının
Uzunluğu
Ortak teğet uzunluğunun
bulunabilmesi için merkezlerden teğetlere dikler çizilir.
O1O2C
dik üçgeninde |CO2|
= |AB|
| |AB|2
=|O1O2|2
- |r1-r2|2 |
5. Bir Doğru İle Bir
Çemberin Durumları
Aynı düzlemde bulunan O
merkezli r yarıçaplı bir çember ile d doğrusu üç
farklı durumda bulunur.
|
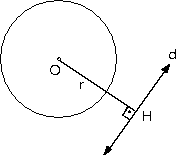
a. |OH| > r ise
doğru çemberi kesmez
ve doğru çemberin dışındadır.
Çember Ç
d = Æ
|
|
|
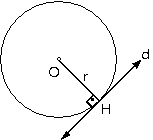
b. |OH| = r ise
doğru çemberi bir
noktada keser. Yani doğru çembere teğettir.
Çember Ç
d = {H}
|
|
|
c. |OH| < r ise
doğru çemberi iki
noktada keser.
Çember Ç
d = {A, B}
|
 |