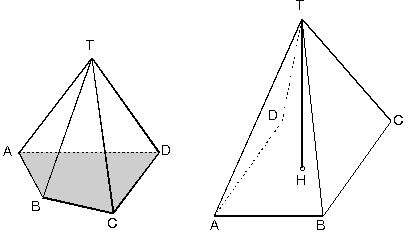
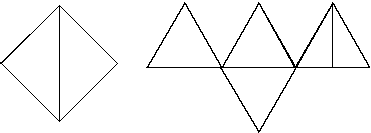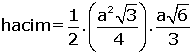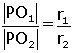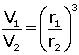Bir düzlemde kapalı bir bölge ile bu düzlemin dışında bir T noktası alalım. Kapalı bölgenin tüm noktalarının T noktası ile birleştirilmesi sonucunda oluşan cisme piramit denir.
T noktası piramidin tepe noktasıdır. Kapalı bölge ise piramidin tabanıdır. Piramit; tabanı oluşturan şeklin ismiyle adlandırılır. Taban kare ise, kare piramit; taban altıgense altıgen piramit gibi. Eğer piramidin tabanı düzgün çokgense bu tip piramitlere düzgün piramit denir. T noktasının taban düzlemi üzerindeki dik izdüşümüne H dersek [TH] piramidin yüksekliği olur. |TH| = h biçiminde yazılır. [TA], [TB], [TC] piramidin yanal ayrıtlarıdır. Piramitlerin hacmi taban alanı ile yüksekliğin çarpımının üçte biri kadardır.
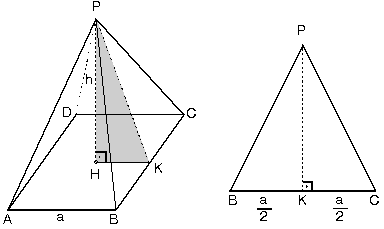
1.Kare Piramit
Kare piramidin tabanı kare biçimindedir. Yan yüzeyleri ise dört adet ikizkenar üçgenden oluşur. İkizkenar üçgenlerin taban uzunlukları piramidin tabanının bir kenarına eşittir. |PH| = h piramidin yüksekliğidir. Yan yüz yüksekliği |PK| dır. Tabanının bir kenarına a dersek
Buradan yan yüz yüksekliği |PK|2
= h2
+ (
Tüm alan yan yüz alanları ile taban alanının toplamına eşittir.
2. Eşkenar Üçgen Piramit Tabanı eşkenar üçgen olan piramitlere eşkenar üçgen piramit denir.
3. Düzgün Dörtyüzlü
Dört yüzü de eşkenar üçgenlerden oluşan cisimdir. Yükseklik, tabanı oluşturan üçgenin ağırlık merkezine iner. Bir ayrıtı a olan düzgün dörtyüzlünün
Buradan
4. Düzgün Sekizyüzlü
Piramitin hacmi
Yüzey şekilleri eşkenar üçgen olduğundan
5. Düzgün Altıgen Piramit Tabanı düzgün altıgen olan piramide düzgün altıgen piramit denir. Yan yüzeyleri altı adet eş ikizkenar üçgenden oluşur. KONİ Tabanı daire biçiminde olan piramide koni adı verilir.
bulunur. Yan yüzeyleri altı adet eş ikizkenar üçgen oluşur. KONİ
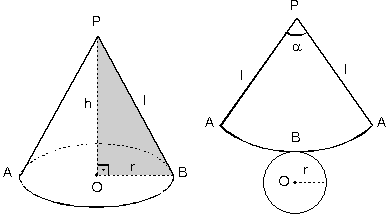
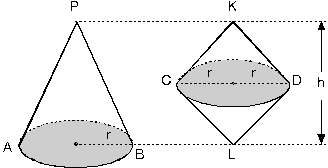
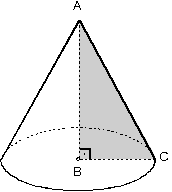
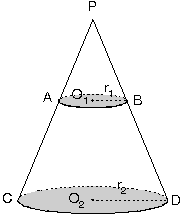
Tabanı daire biçiminde olan piramite koni adı verilir. Burada; Taban yarıçapı |OB| = r Cisim yüksekliği |PO| = h olur. |PA| = |PB| = l uzunluğuna ana doğru denir. POB dik üçgeninde, h2 + r2 = l2 bağıntısı vardır. Koninin yanal alanı bir daire dilimidir.
Daire diliminin alanı, yay uzunluğu ile yarıçapın çarpımının yarısıdır. Yay uzunluğu taban çevresine eşit olduğundan, Yanal alan= pr2+prl Tüm alan bulunurken, taban alanı da ilave edilir. Tüm alan = r2 + rl
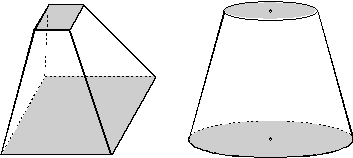
Kesik piramitlerin hacimleri bulunurken cisim piramide tamamlanır.
KÜRE
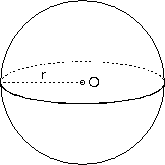
O merkezli R yarıçaplı kürede;
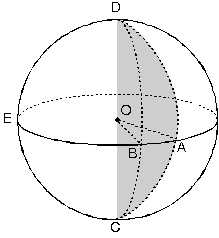
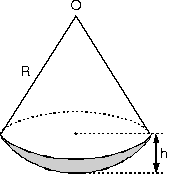
1. Küre Dilimi
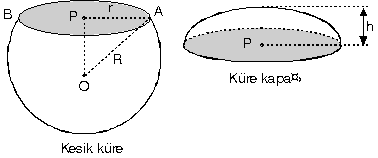
2. Küre Kapağı
Bir küre merkezinden |OP| uzaklıkta bir düzlemle kesildiğinde kesit alanının daire şeklinde olduğu görülür. Kesilip çıkarılan kısma küre kapağı denir. Kesitin merkezinden uzaklığına |OP|, kesitin yarıçapına r ve kürenin yarıçapına R dersek
|