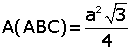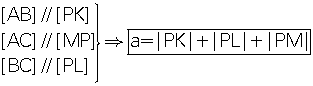| Bir açısının
ölçüsü 90° olan üçgene dik üçgen denir. Dik üçgende
90° nin karşısındaki kenara hipotenüs, diğer
kenarlara dik kenar adı verilir. Hipotenüs üçgenin daima
en uzun kenarıdır.
şekilde, m(A) = 90°
[BC] kenarı hipotenüs
[AB] ve [AC] kenarları
dik kenarlardır.
|
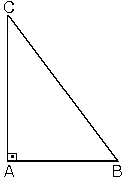 |
| Dik üçgende dik kenarların
uzunluklarının kareleri toplamı hipotenüsün
uzunluğunun karesine eşittir.
ABC üçgeninde m(A) = 90°
|
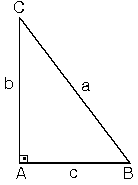 |
1. (3 - 4 - 5) Üçgeni
|
Kenar uzunlukları (3
- 4 - 5) sayıları veya bunların katı olan bütün
üçgenler dik üçgendir. (6 - 8 - 10), (9 - 12 - 15),
gibi
|
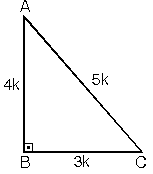 |
2. (5 - 12 - 13) Üçgeni
|
Kenar uzunlukları (5 - 12 - 13) sayıları
ve bunların katı olan bütün üçgenler
dik üçgenlerdir. (10 - 24 -
26), (15 - 36 - 39),
gibi.
|
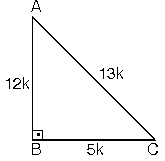 |
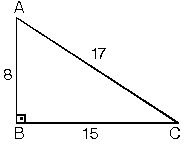
| Kenar uzunlukları
8, 15, 17 sayıları ile orantılı olan üçgenler
dik üçgenlerdir. |
 |
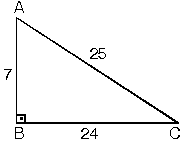
| Kenar uzunlukları 7, 24,
25 sayıları ile orantılı olan üçgenler dik
üçgenlerdir. |
 |
3. İkizkenar dik üçgen
|
ABC dik üçgen |AB| = |BC| = a
|AC| = aÖ2
m(A) = m(C) = 45° İkizkenar dik
üçgende
hipotenüs dik kenarların Ö2
katıdır.
|
![]() |
4. (30° 60° 90°) Üçgeni
|
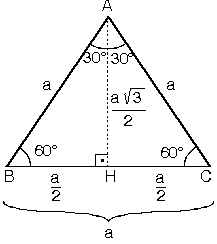
ABC eşkenar üçgeni yükseklikle
ikiye bölündüğünde
ABH ve ACH (30° - 60° - 90°)
üçgenleri elde edilir.
|AB| = |AC| = a
| |BH| = |HC| = |
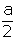 |
| pisagordan |
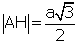 |
|
 |
| (30° - 60° - 90°) dik üçgeninde;
30°'nin karşısındaki kenar
hipotenüsün yarısına eşittir.
60° nin karşısındaki kenar,
30° nin karşısındaki
kenarın Ö3
katıdır.
|
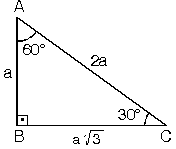 |
| 5. (30° - 30° - 120°)
Üçgeni
(30° - 30° - 120°)
üçgeninde 30° lik açıların karşılarındaki
kenarlara a dersek 120° lik açının karşısındaki
kenar aÖ3 olur.
|
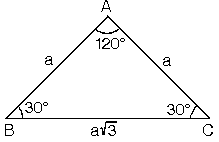 |
| 6. (15° - 75° - 90°)
Üçgeni
(15° - 75° - 90°) üçgeninde
hipotenüse ait yükseklik |AH| = h
dersek, hipotenüs
|BC| = 4h olur. Hipotenüs
kendisine ait yüksekliğin dört
katıdır.
|
 |
| Dik üçgenlerde hipotenüse
ait yüksekliğin verildiği durumlarda benzerlikten
kaynaklanan öklit bağıntıları kullanılır. |
 |
1. Yüksekliğin hipotenüste ayırdığı
parçaların çarpımı yüksekliğin karesine eşittir.
3. ABC üçgeninin alanını iki
farklı şekilde yazıp eşitlediğimizde
- Yukarıda anlatılan öklit bağıntıları
kullanılarak
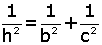 elde
edilir. elde
edilir.
Genellikle bu öklit bağıntısını kullanmak
yerine, yukarıdaki öklit bağıntıları ve
pisagor bağıntısını kullanarak çözüme
gideriz.
| İkizkenar üçgenin tepe
açısından tabanına çizilen yükseklik, hem açıortay,
hem de kenarortaydır. |
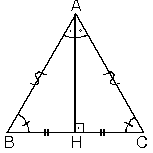 |
| 1. Bir üçgende, açıortay
aynı zamanda yükseklik ise bu üçgen ikizkenar üçgendir.
|AB| = |AC|
|BH| = |HC|
m(B) = m(C)
|
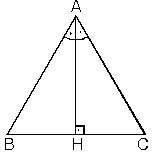 |
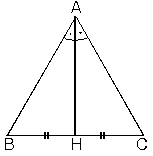
| 2. Bir üçgende, açıortay
aynı zamanda kenarortay ise bu üçgen ikizkenar üçgendir.
|AB| = |AC|,
[AH] ^
[BC]
m(B) = m(C)
|
 |
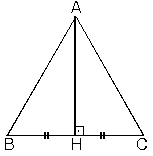
| 3. Bir üçgende, yükseklik
aynı zamanda kenarortay ise bu üçgen ikizkenar üçgendir.
|AB| = |AC|
m(BAH) = m(HAC)
m(B) = m(C)
|
 |
| İkizkenar üçgende açıortay,
kenarortay ve yüksekliğin aynı olması birçok
yerde karşımıza çıktığından
çok iyi bilinmesi gereken bir özelliktir. |
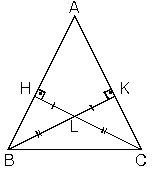
| 4. İkizkenar üçgende
ikizkenara ait yükseklikler eşittir. Bu durumda yüksekliklerin
kesim noktasının ayırdığı parçalarda
eşit olur. |
 |
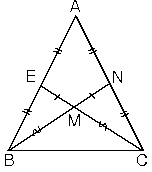
| 5. İkizkenar üçgende
ikizkenara ait kenarortaylar ve kenarortayların kesim
noktasının ayırdığı parçalar da
birbirine eşittir. |
 |
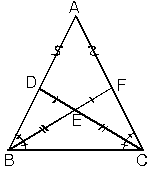
| 6. İkizkenar üçgende
eşit açılara ait açıortaylar da eşittir. Açıortaylar
birbirini aynı oranda bölerler. |
 |
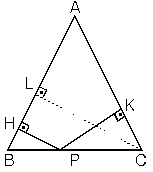
| 7. İkizkenar üçgende
ikiz olmayan kenar üzerindeki herhangi bir noktadan ikiz
kenarlara çizilen dikmelerin toplamı, ikizkenarlara ait yüksekliği
verir.
| |AB| = |AC| Þ
|LC| = |HP| + |KP| |
|
 |
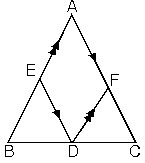
| 8. İkizkenar üçgende
tabandan ikiz kenarlara çizilen paralellerin toplamı, ikiz
kenarların uzunluğuna eşittir.
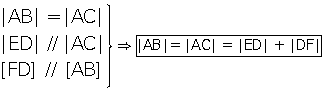
|
 |
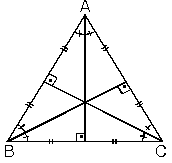
EŞKENAR ÜÇGEN
| 1. Eşkenar üçgende
bütün açıortay, kenarortay yükseklikler çakışık
ve hepsinin uzunlukları eşittir.
nA
= nB
= nC
= Va
= Vb
= Vc
= ha
= hb
= hc
|
 |
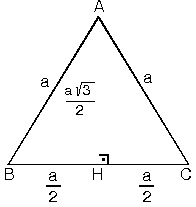
| 2. Eşkenar üçgenin
bir kenarına a dersek yük seklik
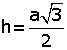 Bu durumda eşkenar üçgenin alanı
Bu durumda eşkenar üçgenin alanı
|
 |
yükseklik cinsinden alan değeri
Alan(ABC) = 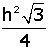
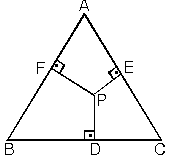
| 3. Eşkenar üçgenin
içindeki herhangi bir noktadan kenarlara çizilen dik
uzunlukların toplamı, eşkenar üçgene ait yüksekliği
verir.
Bir kenarı a olan eşkenar üçgende;
|
 |
| 4. Eşkenar üçgenin
içindeki herhangi bir noktadan kenarlara çizilen paralellerin
toplamı bir kenar uzunluğuna eşittir. |
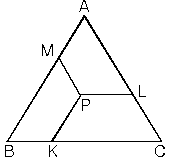 |
Bir kenarı a olan ABC eşkenar üçgeninde
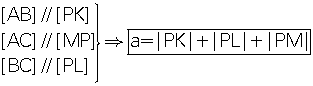
|
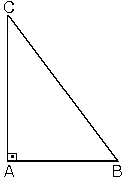
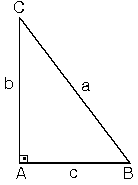
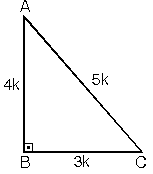
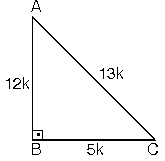



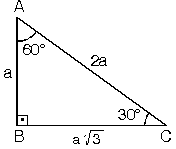
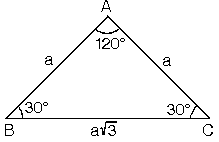










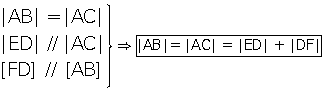


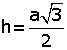 Bu durumda eşkenar üçgenin alanı
Bu durumda eşkenar üçgenin alanı